CADA GRUPO DEVE SER RESOLVIDO EM FOLHAS SEPARADAS.

A duração do exame é de 3 h. Responda às seguintes questões apresentando os cálculos que efectuar e JUSTIFICANDO as respostas dadas. Nunca fique ‘preso’ em nenhuma resposta; se necessário, passe à frente para regressar mais tarde à mesma questão. Boa sorte !

As notas desta prova sairão até às 14 h do dia 16 de Janeiro (4ª feira), no placard da cadeira e a revisão de provas será às 14 h do dia 18 de Janeiro (6ª feira), junto à Secretaria da Secção de Telecomunicações.

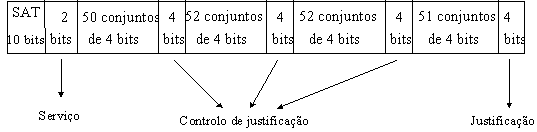
Considere a estrutura de trama da 2^a hierarquia plesiócrona (CEPT3) do CCITT (8.448 Mbit/s):

a) Determinar a duração da trama. (R: 100,33 us)
b) Determinar a taxa máxima de justificação (em bit/s), por tributário. (R: 9,96 kbit/s)
C) O sinal de alinhamento de trama (SAT) é considerado incorrecto desde que um ou mais bits desse sinal sejam recebidos com erro. Supondo que se declara a perda de sincronismo de trama quando são recebidos 3 SAT’s consecutivos errados e que a probabilidade de erro de bit no canal de transmissão é de 10^-4, calcular o tempo médio entre declarações indevidas de perda de sincronismo de trama. (R: 1,16 dias)
 
 

Uma fonte quaternária emite símbolos a uma taxa de 1000 símbolos por segundo. Os símbolos são transmitidos através de um canal com uma capacidade de 1700 bit/s.

a) Qual o ritmo de informação máximo possível à saída da fonte (em bit/s) ? (R: 2000 bit/s)
b) Suponha que as probabilidades dos símbolos emitidos são 2/3, 1/6, 1/12 e 1/12. i) Determinar uma tabela de codificação de Huffman simples (1^a ordem) e calcular a eficiência de codificação que se obtém. ii) Como se poderia melhorar esta eficiência, mantendo o tipo de codificação (Huffman) e a suposição de símbolos independentes? Justifique. (R: 94,88 %; extensão de 2ª ordem)
c) Para as probabilidades dos símbolos indicadas em b), será possível, com codificação adequada, transmitir a saída da fonte pelo canal referido, com uma probabilidade de erro arbitrariamente pequena na recepção? (Admita que a única fonte de distorção do sinal é ruído aditivo, branco e gaussiano). (R: Sim)
 
 

Um sistema de áudio estéreo (dois canais), é digitalizado utilizando PCM uniforme e uma frequência de amostragem de 44,1 kHz por canal. A potência média normalizada do sinal de áudio é de 0,5 (a tensão de corte normalizada do quantificador é ± 1). O quantificador tem 65536 níveis de quantificação.

a) Determinar o valor da relação sinal-ruído de quantificação (S/N_q) resultante da conversão A/D do sinal áudio. (R: 98 dB)
b) Determine: i) o débito binário total gerado pela digitalização do sinal; ii) a largura de banda mínima necessária para a transmissão do sinal digitalizado, através de um canal passa-baixo ideal. (R: 1,411 Mbit/s; 705,6 kHz)
c) Quantos minutos de música (já digitalizada) poderão ser gravados num CD com uma capacidade de 750 Mbytes? Admita que 1/6 da capacidade do CD está reservada para sincronização e códigos correctores de erros. (R: 59,1 minutos)
 
 

Suponha uma ligação por feixes hertzianos digitais, a 5 GHz, na distância de 40 km, com uma potência emitida de 2,5 W e usando antenas parabólicas.

a) Calcule o ganho de cada uma das antenas (emissão e recepção), supostas iguais, para que a potência de sinal à entrada do receptor, em condições ideais de propagação, seja de -25 dBm. (R: 39,7 dB)
b) Indique quanto varia a margem uniforme, em relação à situação da alínea anterior, se o ganho de cada antena aumentar 2 dB e a largura de banda equivalente de ruído aumentar 35%. (R: 2,7 dB)
c) Sabendo que para uma das cláusulas da ITU-R, a margem uniforme é de 35 dB, a margem selectiva é de 25 dB e a margem real mínima é de 30 dB, quais as principais acções que podem ser tomadas no sentido da ligação verificar essa cláusula? Justifique. (R: Diversidade e igualação)
 
 

Considere uma comunicação videotelefónica, segundo a norma ITU-T H.261, usando um débito binário de 40 kbit/s. A sequência é codificada usando a resolução espacial CIF e uma frequência de imagem de 10 Hz.
A imagem que tem de transmitir está dividida horizontalmente em 4 partes iguais, sendo as 2ª e última faixas fixas e as 1ª e 3ª partes com movimento. Atendendo a que o codificador faz uma codificação sequencial dos macroblocos, constata-se que os bits de código são gerados uniformemente, nos vários intervalos em que há informação para codificar, não sendo gerados bits nos períodos correspondentes a zonas fixas, com excepção da primeira imagem onde os bits são gerados uniformemente em toda a imagem. Posteriormente à primeira imagem, a faixa da imagem mais acima tem uma menor actividade que a 3ª faixa que se traduz por uma produção de bits que, para cada imagem, é sempre tripla da faixa mais acima, menos activa. Admita que o tempo gasto na codificação de cada faixa é constante e igual a ¼ do período da imagem.
No codificador, os bits de código aguardam a sua transmissão na memória de saída. Sabendo que na codificação da primeira imagem se gastaram 15000 bit, na da segunda 20000 e na da terceira 8000, calcule, justificando:

a) O instante em que o receptor obtém todos os bits de código correspondentes à 2ª imagem. (R: 875ms)
b) A dimensão mínima da memória de saída do codificador para que nunca haja perda de bits na situação acima descrita. (R: 32000 bit)
c) O atraso inicial de visualização mínimo (contado a partir do instante de aquisição da 1^a imagem), a aplicar no descodificador, supondo que tem disponível à saída do codificador metade da memória determinada na alínea anterior e que o codificador passa a produzir os bits de código para cada imagem, instantaneamente no momento da sua aquisição (codificação infinitamente rápida). (R: 400 ms)
 

a) Para que gama de distâncias o protocolo A é mais eficiente (em tempo) que B? Efectue o estudo na ausência de erros e supondo que se pretendem enviar 100 MBytes. (R: d<= 45 km)
b) Considere agora uma ligação lógica, conforme a família de protocolos HDLC, em que se adoptou o polinómio  para o cálculo dos campos de controlo de erro. A bandeira (flag) é: 0111 1110. Supondo que ao receptor chega a seguinte sequência de bits:

Recupere a mensagem recebida pelo receptor e conclua sobre a existência ou não de erros na transmissão. Admita que os bits de maior peso são os mais à esquerda. (R: não há erros)
c) Dê um exemplo em que ocorrendo 4 erros na mensagem acima recebida (indicando em que bits) ela é ainda assim detectada como correcta. Demonstre esse facto.
 
 

n_q=q²/12 - ruído de quantificação uniforme
E_b/N₀ [dB]=C/N [dB] + 10 log (B_W/f_b)
Lfs [dB] = 32.4 + 20 log₁₀ d (km) + 20 log₁₀ f (MH_z) - atenuação em espaço livre
N₀ [dB_W]= 10 log₁₀ (K T B_w); K= 1.38 x 10^-23 J/K - potência de ruído térmico
G [dB] = 20 log₁₀ ( p .D / l ) + 10 log₁₀ h - ganho de uma antena parabólica
a = (l ² / 4p ) . g – abertura efectiva de uma antena