IMPRESSÃO DIGITAL ÁUDIO

Os sistemas de impressões digitais têm mais de cem anos de idade. Em 1893, Sir Francis Galton foi o primeiro a "provar" que não existem duas impressões digitais nos seres humanos iguais. Cerca de 10 anos mais tarde, a Scotland Yard aceitou um sistema desenhado por Sir Edward Henry para identificação de impressões digitais de pessoas. Este sistema baseia-se no desenho formado pelas papilas (elevações da pele), presentes nas polpas dos dedos das mãos e ainda é usado como base em todos os sistemas de identificação de impressões digitais em pessoas nos dias de hoje.

No caso do áudio é também possível extrair uma impressão digital de qualquer música sendo esta também única.

Uma maneira simples de obter uma impressão digital de um arquivo digital é a utilização de um algoritmo de hashing no fluxo de bits, mas isso não irá fornecer um hash consistente para diferentes formatos ou codecs de áudio. Este sistema também não permite identificar ficheiros ruidosos ou apenas uma pequena parte de uma música. Em vez disso, o que se faz é construir uma impressão digital das características preceptivas da música. Este processo de identificação de uma música depende assim exclusivamente do seu conteúdo de áudio.

Estes sistemas de obtenção de impressões digitais têm que ser resistentes às diferenças entre o sinal de áudio usado para fazer a base de dados inicial e o sinal utilizado na pesquisa e também à degradação do sinal devido às transmissões nas redes de rádio ou redes de telefone. O ruído de fundo de uma festa ou outros barulhos ambientes têm que ser ignorados. Finalmente, as diferenças de amplitude devido a efeitos, tais como equalização ou compressão não devem afetar o sucesso da obtenção da impressão digital de uma música.

Ao contrário dos metadados, as impressões digitais de áudio usam a própria informação gravada para identificar a música. Alguns usos comuns destes sistemas são:

• Detecção de conteúdo com direitos de autor: Por exemplo o Youtube usa um sistema de identificação de conteúdo (Content ID system[9]) para determinar se um vídeo contém áudio com direitos de autor e fornece uma opção para o utilizador que publicou esse video de bloquear o áudio do vídeo ou para exibir anúncios junto com a reprodução.
• Identificação de uma música: Pessoas ao ouvirem uma música no rádio ou em uma festa podem querer saber que música é. O sistema de identificação precisa assim de ser capaz de lidar com sinais ruidosos e que faça a identificação a partir de qualquer parte da música. Por exemplo, o Shazam[10] fornece uma aplicação para smartphones que realiza este processo.
• Organização de uma biblioteca de música: Às vezes, os metadados de um ficheiro podem não ser precisos. Uma forma de corrigir os metadados é identificar a música pelo seu conteúdo na base de dados de impressões digitais, para reformular os metadados. Por exemplo, o MusicBee[11] é uma ferramenta que permite aos utilizadores, organizar os seus albums de música dessa maneira.
• Identificação de músicas para a verificação de royalties: As estações de rádio podem ter um sistema que identifique todas as músicas que foram transmitidas, com a finalidade de relatar contagens para as agências de cobrança de direitos de autor.

O processo

O processamento da impressão digital é dividido em um certo número de passos. Diferentes algoritmos de impressão digital de áudio, muitas vezes realizam processos diferentes em cada etapa, embora, em geral, o processo segue um padrão semelhante.

O processamento normaliza todas as amostras a um denominador comum. É comum transformar todos os canais para um sinal mono e reduzir taxa de amostras. A taxa varia de algoritmo para algoritmo, mas os valores comuns são de 11.025kHz ou 5.5125kHz.

Extracção de características

O processo de extracção de características estabelece os componentes de um sinal que vão ser usados para gerar a impressão digital.

O primeiro passo de extracção de características é o de gerar um espectrograma do sinal da fonte. O espectrograma é feito a partir de curtas amostras sobrepostas. Muitos algoritmos usam janelas de cerca de 300ms sobrepondo a cada 11ms. Com uma taxa de amostra de 11.025kHz, uma janela de 4096 amostras e 128 amostras de sobreposição daria valores próximos desse tempo.

O processo de identificação de características do espectograma é onde a maioria dos algoritmos diferem uns dos outros.

Por exemplo, o Shazam[10] encontra pontos no espectrograma (usando a transformada rápida de Fourier) onde a amplitude é mais elevada do que picos ao redor.

Devido à alta amplitude, esses pontos também se veem através de dados ruidosos, ou dados que se alteraram as amplitudes, por exemplo, através da equalização. O Shazam gera hashes destas “constelações“ através da codificação da diferença de frequência e tempo entre os pontos mais próximos.

Cada ponto no gráfico representa a intensidade de uma dada frequência de um determinado ponto no tempo. Assumindo que o tempo está no eixo dos x e a frequência está no eixo dos y, uma linha horizontal representaria um tom puro contínuo e uma linha vertical representa uma explosão instantânea de ruído branco.

A maior parte dos algoritmos de extracção de impressões digitais são baseados na seguinte abordagem. Primeiro o sinal de áudio é segmentado em frames. Para cada frame um conjunto de características é computado.

A representação compacta de um único frame será referida como uma sub-impressão digital. Uma sub-impressão digital normalmente não contém dados suficientes para identificar uma música. A unidade de base que contém dados suficientes para identificar uma música será referido como um bloco de impressão digital.

Na experiencia de J.A. Haitsma[14], extrai-se sub-impressões digitais de 32 bits para cada intervalo de 11,8 milissegundos. Um bloco de impressão digital é constituído por 256 sub-impressões digitais, o que corresponde a uma granularidade de apenas 3 segundos. Uma visão geral do sistema é mostrada na Figura 5.

Os frames sobrepostos têm um comprimento de 0,37 segundos. Esta estratégia resulta na extracção de uma sub-impressão digital para cada 11,6 milissegundos. No pior dos casos os limites do quadro utilizados durante a identificação são 5,8 milissegundos, fora o que diz respeito aos limites utilizados na base de dados de impressões digitais pré-computados. A grande sobreposição garante que, mesmo nos casos de pior cenário, as sub-impressões digitais a serem identificadas ainda são muito semelhantes às sub-impressões digitais da mesma amostra na base de dados.

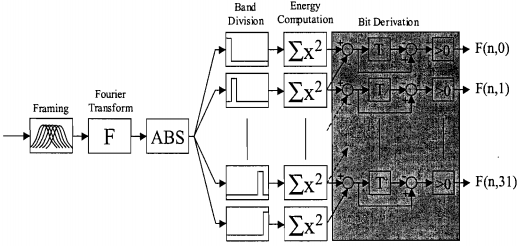
As características de áudio perceptuais mais importantes são no domínio da frequência. Por conseguinte, uma representação espectral é calculada através da transformada de Fourier para cada frame.

Na análise a janela de frequência é dividida em 33 sub-bandas distintas. Se representarmos a energia da banda m do frame n por E (n, m) e o mº bit da sub-impressão digital do frame n por F (n, m), os bits da sub-impressão digital estão formalmente definidos como (ver também o bloco cinza na Figura 6, onde T é um elemento de atraso):

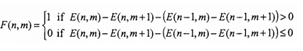
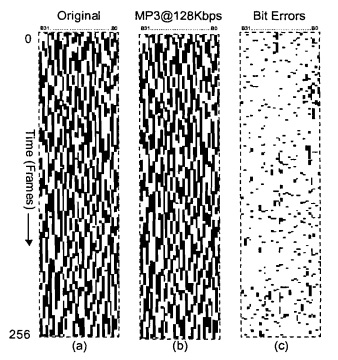
A Figura 5 mostra um exemplo de um bloco de impressões digitais, extraídas com o esquema anterior a partir de um curto trecho de "0 Fortuna" por Carl Orff. Um bit ‘1’ corresponde a um pixel branco e um bit ‘0’ corresponde a um pixel preto. A Figura 5a e Figura 5b mostram um bloco de impressão digital de um CD original e a versão comprimida MP3 (128Kbps) do mesmo trecho, respectivamente. Idealmente, estas duas figuras deviam ser idênticas, mas, devido à compressão alguns dos bits são recuperados de forma incorrecta. Estes erros de bits, que são utilizados como a medida de similaridade para o sistema de impressão digital, são mostrados a preto na Figura 5c.

Podemos ver a arquitectura do sistema na figura 7.

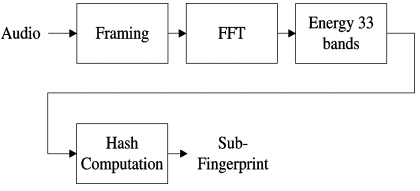
Procura na base de dados

Encontrar impressões digitais já processadas numa base de dados não é uma tarefa trivial. Em vez de procurar uma impressão digital exactamente igual em termos de bits, a impressão digital mais semelhante tem que ser encontrada.

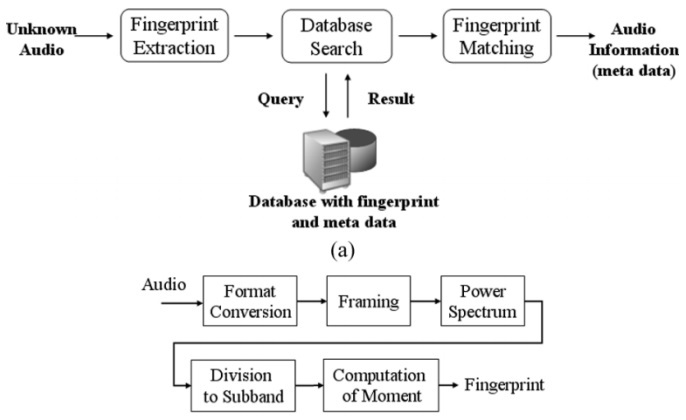
No trabalho de A.J. Haitsma [14] assumem que pelo menos uma das sub-impressões digitais da query de áudio não foi afectada por ruído. Assim a primeira pesquisa é sobre o resultado da função de dispersão (hash) usada sobre a sub-impressão digital. Isto faz com que a primeira pesquisa seja rápida pois não obriga a descodificar todas as músicas para encontrar uma relação perfeita entre a impressão digital e sub-impressões digitais de todas as músicas. Depois de achados os candidatos na tabela de dispersão, músicas que apresentam pelo menos uma sub-impressão digital exactamente igual a uma sub-impressão digital da amostra a ser testada, os frames temporais restantes da amostra serão testados, música a música, tendo em conta a probabilidade de aquela música corresponder à música da amostra. Isto é, se aquando do primeiro varrimento da pesquisa uma música tiver a si associadas mais frames temporais da amostra que as outras músicas, essa música é então entendida como a maior candidata a ser a música correcta, dessa forma ela é a primeira a ser testada. O mesmo se aplica a cada música.

Pode se verificar na figura 8 como é feita a pesquisa na base de dados.